Low Displacement Rank Dictionaries

Displacement structure¹ is a generic procedure to quantify the level structure in a matrix. It defines a certain operation (displacement operator) that transform structured matrices into low-rank matrices. The displacement structure framework also provides fast computational algorithms for operations involving these structured matrices.

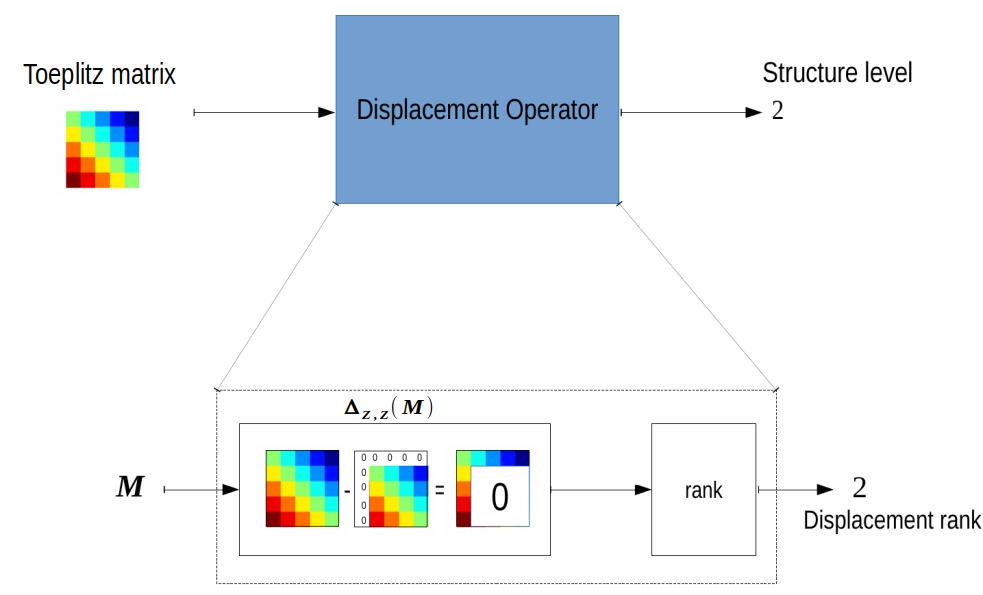
Besides coping with explicit families of structured matrices like Toeplitz, Hankel, Vandermonde and Cauchy, it also manages to identify implicit structure like the inverse or products of structured matrices.

This work was developed during my Master’s degree:

C. F. Dantas, “Learning Structured Dictionaries.” At University of Campinas, 2016.

It includes a black-and-white image denoising demo.

Related slides here.

1. T. Kailath, S.Y. Kung, M. Morf, “Displacement ranks of a matrix”. 1979. ↩