HO-SuKro
A Kronecker product of K matrices corresponds to a separable operator acting on vectorized multimodal data of order K, in the sense that each of the K operators apply independently in the corresponding mode of the K dimensional tensor data (via a tensor mode product).
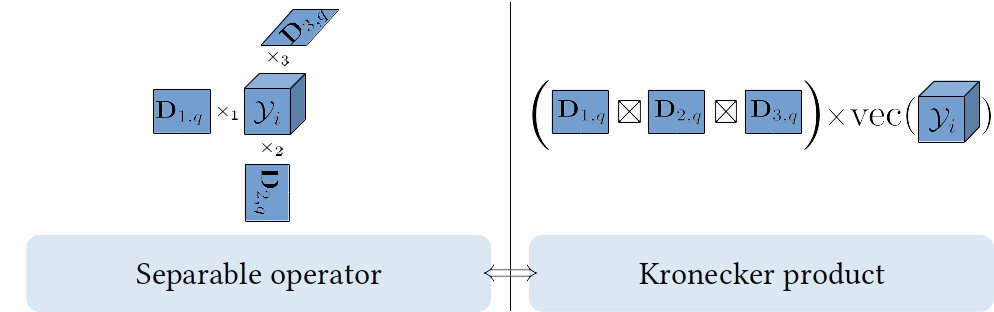
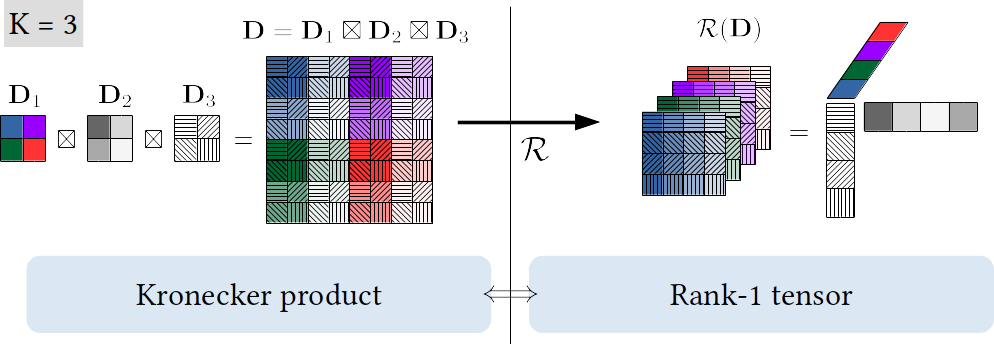
Additionally, such separable operators (Kronecker products) correspond to rank-1 tensors up to an isomorphism (entries rearrangement).
We therefore generalize the concept of separable operators by allowing for a sum of R Kronecker products which corresponds to the more expressive class of rank-R tensor operators.
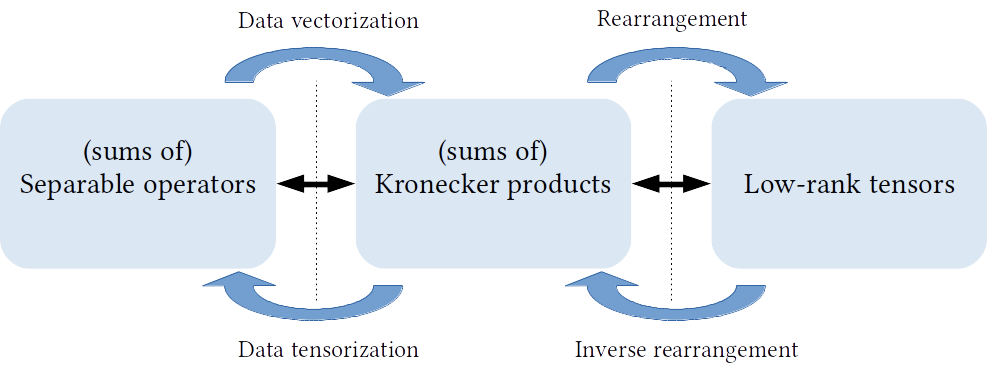
We refer to the resulting sum of R Kronecker products of K factors as (R,K)-KS matrices.
Two distinct approaches for enforcing this higher-order Kronecker structure are listed below. The more recent ALS approach is the faster and more efficient one in general.
Alternate Least Squares Approach Code
This code corresponds to the following paper:
C.F. Dantas, J.E. Cohen, and R. Gribonval. “Learning Tensor-structured Dictionaries with Application to Hyperspectral Image Denoising.” In European Signal Processing Conference (EUSIPCO), 2019.
It includes a hyperspectral image denoising demo (a more advanced hyperspectral image denoising algorithm is described here).
Projected Gradient Approach Code
This code corresponds to the following paper:
C.F. Dantas, J.E. Cohen, and R. Gribonval. “Learning fast dictionaries for sparse representations using low-rank tensor decompositions.” In International Conference on Latent Variable Analysis and Signal Separation (LVA/ICA), 2018.
It includes a color image denoising demo.
Despite being generally heavier than the ALS algorithm above, this approach provides a projection operator on the space of (R,K)-KS matrices, which can be useful when tackling more generic problems.
